KL 散度（Kullback-Leibler Divergence）：图示+公式+代码

本文通过融合图表示例、公式和代码的多元化方式阐释 KL 散度，希望对大家从理论到实践，全面理解 KL 散度有一定帮助。

本文内容

示例数据
信息熵（Information Entropy）的简介
KL 散度的计算公式
二进制编码角度的解释
KL 散度的分步计算
KL 散度的特点及代码示例
作为损失函数

示例数据

如下为后面用到的示例数据。

import matplotlib.pyplot as plt  

# 在MacOS 中指定字体
plt.rcParams['font.family'] = ['Songti SC', 'Arial', 'Helvetica', 'Times New Roman']
plt.rcParams['font.size'] = 8

# 假设一个盒子中有七个颜色的球（红橙黄绿青蓝紫），对应的真实概率分别是
box_p = [0.15, 0.13, 0.23, 0.09, 0.2, 0.05, 0.15]  

# 有两个机器学习程序，根据从盒子中取出来的球的颜色推断概率如下
box_q1 = [0.14, 0.14, 0.25, 0.08, 0.21, 0.06, 0.12]  
box_q2 = [0.11, 0.11, 0.22, 0.16, 0.15, 0.16, 0.09]  
# print(sum(box_p), sum(box_q1), sum(box_q2))

if __name__ == "__main__":
    # 图表展示出来
    indices = range(len(box_p))  
    fig, ax = plt.subplots()
    width = 0.25
    ax.bar(range(len(box_p)), box_p, width=width, label='真实概率')  
    ax.bar([i+width for i in range(len(box_p))], box_q1,  width=width, label='预测概率 1')  
    ax.bar([i+width*2 for i in range(len(box_p))], box_q2,  width=width, label='预测概率 2')  
    plt.xlabel('颜色编号')  
    plt.ylabel('概率')  
    plt.title('数据示例 - 真实概率和预测概率')  
    plt.legend()
    plt.show()

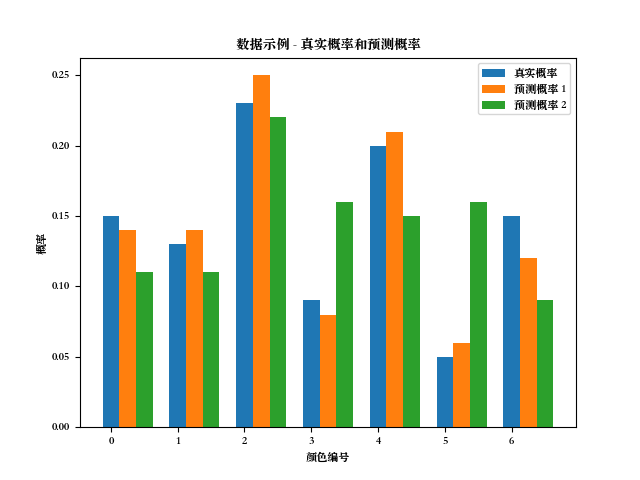
用图表展示的数据如下：

信息熵（Information Entropy）的简介

KL散度（Kullback-Leibler Divergence）起源于信息理论。信息理论的主要目标是量化数据中的信息量。信息理论中最重要的度量标准称为熵（Entropy），通常表示为 $H$ 。对于一个概率分布，熵的定义是：

H=-\sum_{i=1}^Np(x_i)\cdot\log p(x_i)

如果我们在计算中使用 $log_2$ 我们可以将熵解释为“编码我们的信息所需的最小比特数”。

举几个最简单的例子，有一门语言是由 ABCD 四个字母组成的，整个语料库为 8192个字母。

【例1】A、B、C、D 四个字母分别占 1/2（4096个），1/4（2048个），1/8（1024个），1/8（1024个）。那么最有效的一种编码方式为 A(0)，B（10），C（110），D(111)。整个语料库的长度 4096 x 1 + 2048 x 2 + 1024 x 3 x 2 = 14336，平均长度为 14336/8192 = 1.75。和下面代码中的【结果1】一致。

【例2】ABCD 四个字母占比一样多，这样最有效的一种编码方式为 A（00），B（01），C（10），D（11），计算平均长度为2，和代码中的【结果2】一致。

【例3】ABCD 四个字母占比变成了1/8（1024个），1/8（1024个），1/2（4096个），1/4（2048个），这样最有效的一种编码方式为 A（110），B（111），C（0），D（10），计算平均长度为1.75，和代码中的【结果3】一致。

我们用熵的方式计算（代码示例1）：

import math

def cal_entropy_log2(prob_distribution):
    return -sum(p * math.log2(p) for p in prob_distribution)

p = [0.5, 0.25, 0.125, 0.125]
entropy = cal_entropy_log2(p)
print(f"熵: {entropy}")
#【结果1】输出为：熵: 1.75

q = [0.25, 0.25, 0.25, 0.25]
entropy = cal_entropy_log2(q)
print(f"熵: {entropy}")
#【结果2】输出为：熵: 2.0

q2 = [0.125, 0.125, 0.5, 0.25]
entropy = cal_entropy_log2(q2)
print(f"熵: {entropy}")
#【结果3】输出为：熵: 1.75

import numpy as np
def kl_divergence_log2(a, b):
    return sum(a[i] * np.log2(a[i]/b[i]) for i in range(len(a)))

print('KL-divergence_log2(例1 || 例2): %.6f ' % kl_divergence_log2(p, q))
# 输出：KL-divergence_log2(例1 || 例2): 0.250000 

print('KL-divergence_log2(例1 || 例3): %.6f ' % kl_divergence_log2(p, q2))
# 输出：KL-divergence_log2(例1 || 例3): 0.875000 

KL 散度的计算公式

KL散度（Kullback-Leibler散度）是一种衡量两个概率分布之间差异性的度量方法。

KL 散度是对熵公式的轻微修改。假定有真实的概率分布 p （一般指观察值，样本）和近似分布 q（一般指预测模型的输出），那两者的差异如下（离散型）：

\begin{aligned} D_{KL}(p||q) &= \sum_{i=1}^Np(x_i)\cdot(\log p(x_i)-\log q(x_i)) \\ &= \sum_{i=1}^Np(x_i)\cdot log\frac{p(x_i)}{q(x_i)} \end{aligned}

连续性的公式如下：

D_{KL}(p||q)=\int_{-\infty}^{\infty}p(x)\cdot log\frac{p(x)}{q(x)}dx

二进制编码角度的解释

假如用二进制编码长度来解释 KL 散度，KL 散度衡量的是当使用基于 $q(x)$ 的编码而非基于 $p(x)$ 的编码对来自 $p(x)$ 的样本进行编码时，所需的额外比特数的期望值，结果大于等于 0（两个概率分布完全一样时为 0）。

还以【例1】计算 KL 散度（注意：这里对数的底还是取 2，而不是概率中用到的自然底数 e）。当我们使用【例2】的 ABCD 编码方式对例 1 的数据编码时，平均长度显然就是 2，故 KL(例1||例2)=2-1.75=0.25。

当我们使用【例3】的 ABCD 编码方式对【例1】的数据编码时，长度变成了 (4096 * 3 + 2048 * 3 + 1024 * 1 + 1024 * 2 )/8192 = 2.625，故 KL(例1||例3)=2.625-1.75=0.875，和代码中一致，即相对于自身分布的最优编码，用另一个分布的最优编码来编码时，平均额外需要0.875个比特。

KL 散度的分步计算

KL 散度的中间步骤的计算结果可能为正，也可能为负数。

以下为 p 和 q1 的 KL 散度的分步计算结果，可对照上面的数据示例和程序输出看。

p[i]	q[i]	p[i]/q[i]	log(p[i]/q[i])	p[i]*log(p[i]/q[i])
0.15	0.14	1.071429	0.068993	0.010349
0.13	0.14	0.928571	-0.074108	-0.009634
0.23	0.25	0.920000	-0.083382	-0.019178
0.09	0.08	1.125000	0.117783	0.010600
0.2	0.21	0.952381	-0.048790	-0.009758
0.05	0.06	0.833333	-0.182322	-0.009116
0.15	0.12	1.250000	0.223144	0.033472
			求和：	0.006735

分步计算的结果和后面代码中的一致。

如下面代码所示。

import numpy as np
from kl_div_data import box_p, box_q1, box_q2

def kl_divergence_step(a, b):
    return np.array([a[i] * np.log(a[i]/b[i]) for i in range(len(a))])

np.set_printoptions(precision=6)
print(kl_divergence_step(box_p, box_q1))
# 输出：
# [ 0.010349 -0.009634 -0.019178  0.0106   -0.009758 -0.009116  0.033472]

print(kl_divergence_step(box_p, box_q2))
# 输出：
# [ 0.046523  0.021717  0.010224 -0.051783  0.057536 -0.058158  0.076624]

KL 散度的特点及代码示例

KL散度具有以下显著特点：

非对称性：KL散度是非对称的，即从 $P$ 分布到 $Q$ 分布的 KL 散度与从 $Q$ 分布到 $P$ 分布的 KL 散度可能不同。如代码中示例，(p || q1) 和 (q1 || p) 不一样。
非负性：KL散度的值始终为非负数。当且仅当两个概率分布完全相同时，KL散度的值才为零。KL散度值越大，表示两个概率分布越不相似。如代码示例中，相对 p， $q2$ 的 KL 散度比 $q1$ 大，这和图上的直观显示一致。
非度量性：KL散度并不满足度量空间的性质，特别是三角不等式。由于非对称性和非度量性，KL 散度不能用于计算两个分布之间的“距离”或“相似度”。
直观性：KL散度的值越大，表示用一个分布近似另一个分布时引入的信息损失或误差越大。这使得KL散度在度量模型的误差或信息损失方面非常直观。

以下代码列出了 KL 散度的三种实现方式：

简单函数
使用 Scipy rel_entr 函数
使用 Pytorch KLDivLoss

import numpy as np
from scipy.special import rel_entr
from kl_div_data import box_p, box_q1, box_q2

def kl_divergence(a, b):
    return sum(a[i] * np.log(a[i]/b[i]) for i in range(len(a)))

print('KL-divergence(p || q1): %.6f ' % kl_divergence(box_p, box_q1))
# KL 散度没有对称性
print('KL-divergence(q1 || p): %.6f ' % kl_divergence(box_q1, box_p))
# 从计算结果可以看出，概率分布 q2 和 p 的差异明显更大
print('KL-divergence(p || q2): %.6f ' % kl_divergence(box_p, box_q2))

# 使用 Scipy rel_entr 函数
p = np.array(box_p)
q1 = np.array(box_q1)
q2 = np.array(box_q2)
# 和上面函数的计算结果一致
print('rel_entr KL-divergence(p || q1): %.6f ' % sum(rel_entr(p, q1)))
print('rel_entr KL-divergence(p || q2): %.6f ' % sum(rel_entr(p, q2)))
print('rel_entr KL-divergence(q1 || p): %.6f ' % sum(rel_entr(q1, p)))
# 自身的 KL 散度是0
print('rel_entr KL-divergence(p || p): %.6f ' % sum(rel_entr(p, p)))

# -------  输出如下 -------
# KL-divergence(p || q1): 0.006735 
# KL-divergence(q1 || p): 0.006547 
# KL-divergence(p || q2): 0.102684 
# rel_entr KL-divergence(p || q1): 0.006735 
# rel_entr KL-divergence(p || q2): 0.102684 
# rel_entr KL-divergence(q1 || p): 0.006547 
# rel_entr KL-divergence(p || p): 0.000000 

# torch 的写法，参考：https://pytorch.org/docs/stable/generated/torch.nn.KLDivLoss.html
import torch
kl_loss = torch.nn.KLDivLoss(reduction="sum",log_target=False)
# 第 1 个参数为模型的输出，上面直接指定了概率，故增加一次 log
# 第 2 个参数为真实概率
output = kl_loss(torch.log(torch.tensor(q1)), torch.tensor(p))
print(output)
# 输出：
# tensor(0.0067, dtype=torch.float64)

作为损失函数

使用 KL 散度作为损失函数的算法在机器学习和深度学习中非常常见，尤其在处理涉及概率分布的问题时。例如

变分自编码器（VAE）：VAE是一种生成模型，它结合了自编码器的结构和概率图模型。在 VAE 中，KL 散度被用作损失函数的一部分，用于衡量编码器生成的潜在空间分布与先验分布之间的差异。

发布于：2024-03-29 12:00:56 描述有误？我来纠错