IoU、GIoU、DIoU、CIoU 等目标检测损失函数：图示 + 代码

本文通过将图片和代码结合的方式，讲解目标检测算法中常用的 IoU 损失函数。

本文内容

IoU（Intersection over Union）
GIoU（Generalized-IoU）
DIoU（Distance-IoU）
CIoU（Complete-IoU）
YOLOv8 中的实现

在计算对象检测评估指标 mAP（平均精度，mean Average Precision）时，计算 IoU（Intersection over Union）是非常关键的一步。因此，在训练过程中，常用 IoU （或者变体）作为损失函数的一部分。

IoU（Intersection over Union）

论文：UnitBox: An Advanced Object Detection Network （2016.08，UIUC、旷视）

后面的图示说明：

红色边框为 Groud Truth 框（简称 GT）
蓝色边框为预测的框。

IoU 衡量了两个边界框的交集区域与并集区域的比例，计算公式如下：

IoU = \frac{A \cap B}{A \cup B}

显然， $0 \leqslant {IoU} \leqslant 1$ ，当没有重叠区域时取 0，当 GT 和预测框重叠时取 1。

图 1：左上为交集 $A \cap B$ ，右上为并集 $A \cup B$ ，左下为 GIoU 中定义的最小覆盖矩形 $C$ ，右下为 GIoU 中定义的补集 $C \backslash (A \cup B)$ 。

以图 1 为例，IoU 即左上图的绿色填充面积除以右上的淡蓝色填充面积。

各种不同情况下，IoU 的值，如下图：

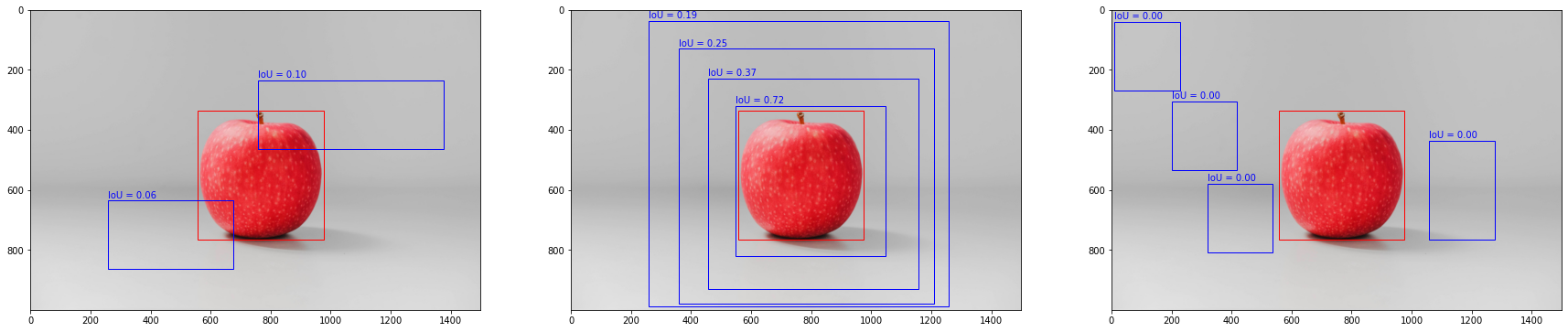图 2：从右图可以看出，对于不相交但是距离有很大差异的情况，IoU 都为 0，故 IoU 对这种情况不能高效收敛。

损失函数的计算（后续 GIoU、DIoU、CIoU 类同）：

\mathcal{L}_{IoU} = 1 - IoU

根据 IoU 的取值范围推算， $0 \leqslant \mathcal{L}_{IoU} \leqslant 1$

【IoU 作为损失函数的不足】

如果两个框没有相交，根据定义，IoU=0，不能反映两者的距离大小（重合度）。
对于框不相交的情况，loss=0，没有梯度回传，无法进行学习训练。（如图2 右图所示）

GIoU（Generalized-IoU）

GIoU 解决了如上 IoU 的不足（两个框不相交的情况）。

论文：Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression （2019.02，斯坦福）

计算公式如下，其中 IoU 的公式和上面相同，C 为能框住 A、B 的最小矩形。

GIoU = IoU − \frac {C \backslash (A \cup B)} {C} \\

显然， $0 \leqslant \frac {C \backslash (A \cup B)} {C} \leqslant 1$ ，故 GIoU 的取值范围为 $[-1,1]$ ，继而损失函数 $0 \leqslant \mathcal{L}_{GIoU} = 1 - GIoU \leqslant 2$ 。

图3：对比图 2，从右图可以看出，GIoU 较好地解决了不相交情况下的距离问题；从中图可以看出，当预测框和 GT 框之间有包含关系时，GIoU 和 IoU 取值相同。

【GIoU 作为损失函数的不足】

在两个预测框有包含关系时，GIoU就退化为IoU，不能反映位置关系。（如图 3 中，图 6-2）

DIoU（Distance-IoU）

为了解决 GIoU 上面的问题，DIoU 通过两个中心点距离和对角线的比值来衡量框的距离关系。这样同时解决了不相交和框包含两种情形下的问题（当然不止于此）。

论文：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression （2019.11，天津大学）

图 4a 边界框回归的 DIoU 损失，其中可以直接最小化中心点之间的归一化距离。c 是覆盖两个框的最小封闭框的对角线长度，d 是两个框的中心点之间的距离。

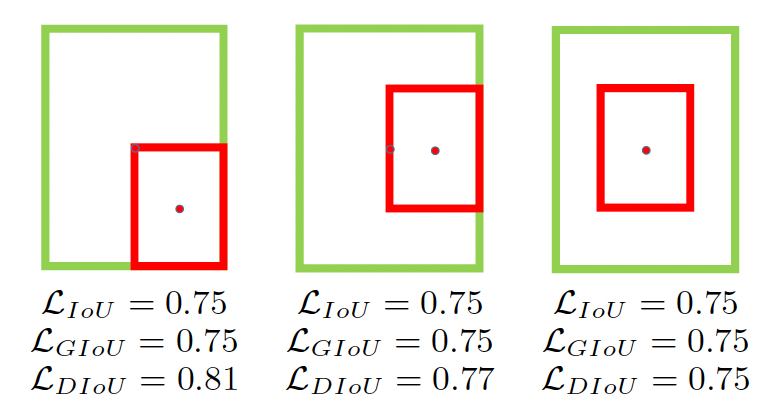图 4b 论文中的示例。GIoU损失降级为IoU损失，DIoU损失仍然可以区分。绿色和红色分别表示目标框和预测框。

公式如下：

DIoU = IoU - \frac {\rho^2(b,b^{gt})}{c^2} \\

其中 $b$ 和 $b^{gt}$ 分别为预测值和 GT 中心点的坐标, $\rho()$ 为欧几里得距离， $c$ 同 GIoU 中 C 的对角线长度。

图 5：DIoU 取值示例

对比 GIoU看，对于预测框在 GT 框内的情况，GIoU 无法区分，但是，考虑中心点距离后，DIoU 可以较好地解决。

图 6：DIoU 考虑了中心点距离和对角线之比，从第2、3图的对比可以看出，DIoU 相比 GIoU，可以表征两个框中心点的距离关系

CIoU（Complete-IoU）

论文和 DIoU 相同。

边界框回归的良好损失应考虑三个重要几何因素，即重叠区域、中心点距离和纵横比。原生的 IoU 损失考虑了重叠区域，GIoU 的损失在很大程度上依赖于 IoU 损失。DIoU损失同时的重叠面积和中心点距离边界框。CIoU损失在DIoU 的基础上，增加了纵横比的一致性要求。

\begin{align*} CIoU &= IoU - \frac {\rho^2(b,b^{gt})}{c^2} - \alpha v \\ 其中，v &= \frac{4}{\pi^2} (arctan\frac{w^{gt}}{h^{gt}} - arctan\frac{w}{h})^2 \\   \alpha &= \frac{v}{(1-IoU) + v} \end{align*}

v 可以理解为，在一个单位圆上，两个框的长、宽构成的角度形成的弧的差异。

对比 DIoU看，对于预测框在 GT 框内，中心点距离相同，形状不同的情况，DIoU 无法区分，但是，考虑形状的长宽对比后，CIoU 可以较好地解决。

图 7：CIoU 考虑了框的长宽比例

YOLOv8 中的实现

IoU 的计算代码非常简洁，如下为 YOLOv8 中的完整代码实现。

import math
import torch

def bbox_iou(box1, box2, xywh=True, GIoU=False, DIoU=False, CIoU=False, eps=1e-7):
    """
    Calculate Intersection over Union (IoU) of box1(1, 4) to box2(n, 4).
    xywh格式的x，y为中心点坐标

    Args:
        box1 (torch.Tensor): A tensor representing a single bounding box with shape (1, 4).
        box2 (torch.Tensor): A tensor representing n bounding boxes with shape (n, 4).
        xywh (bool, optional): If True, input boxes are in (x, y, w, h) format. If False, input boxes are in
                               (x1, y1, x2, y2) format. Defaults to True.
        GIoU (bool, optional): If True, calculate Generalized IoU. Defaults to False.
        DIoU (bool, optional): If True, calculate Distance IoU. Defaults to False.
        CIoU (bool, optional): If True, calculate Complete IoU. Defaults to False.
        eps (float, optional): A small value to avoid division by zero. Defaults to 1e-7.

    Returns:
        (torch.Tensor): IoU, GIoU, DIoU, or CIoU values depending on the specified flags.
    """

    # Get the coordinates of bounding boxes
    if xywh:  # transform from xywh to xyxy
        (x1, y1, w1, h1), (x2, y2, w2, h2) = box1.chunk(4, -1), box2.chunk(4, -1)
        w1_, h1_, w2_, h2_ = w1 / 2, h1 / 2, w2 / 2, h2 / 2
        b1_x1, b1_x2, b1_y1, b1_y2 = x1 - w1_, x1 + w1_, y1 - h1_, y1 + h1_
        b2_x1, b2_x2, b2_y1, b2_y2 = x2 - w2_, x2 + w2_, y2 - h2_, y2 + h2_
    else:  # x1, y1, x2, y2 = box1
        b1_x1, b1_y1, b1_x2, b1_y2 = box1.chunk(4, -1)
        b2_x1, b2_y1, b2_x2, b2_y2 = box2.chunk(4, -1)
        w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
        w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps

    # Intersection area
    inter = (b1_x2.minimum(b2_x2) - b1_x1.maximum(b2_x1)).clamp_(0) * \
            (b1_y2.minimum(b2_y2) - b1_y1.maximum(b2_y1)).clamp_(0)
    # Union Area
    union = w1 * h1 + w2 * h2 - inter + eps
    # IoU
    iou = inter / union
    if CIoU or DIoU or GIoU:
        cw = b1_x2.maximum(b2_x2) - b1_x1.minimum(b2_x1)  # convex (smallest enclosing box) width
        ch = b1_y2.maximum(b2_y2) - b1_y1.minimum(b2_y1)  # convex height
        if CIoU or DIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
            c2 = cw ** 2 + ch ** 2 + eps  # convex diagonal squared
            rho2 = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 + (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4  # center dist ** 2
            if CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
                v = (4 / math.pi ** 2) * (torch.atan(w2 / h2) - torch.atan(w1 / h1)).pow(2)
                with torch.no_grad():
                    alpha = v / (v - iou + (1 + eps))
                return iou - (rho2 / c2 + v * alpha)  # CIoU
            return iou - rho2 / c2  # DIoU
        c_area = cw * ch + eps  # convex area
        return iou - (c_area - union) / c_area  # GIoU https://arxiv.org/pdf/1902.09630.pdf
    return iou  # IoU

发布于：2023-11-20 10:18:58 描述有误？我来纠错