本文通过将图片和代码结合的方式,讲解深度学习反向传播(Backpropagation)的原理。部分内容来源于:Calculus on Computational Graphs: Backpropagation 。
关键要点:
- 反向传播算法主要源于微积分中的链式法则、乘法法则和加法法则等数学思想。
- 反向传播相对前向传播,有很大的性能优势
- Pytorch的实现
本文内容
引言
反向传播是使深度学习模型训练计算上可行的关键算法。相比简单实现,它使基于梯度下降的训练速度提高了百万倍以上,这意味着可以在一周内完成以往需要几十万年的模型训练任务。
反向传播的应用远不止深度学习领域,它实际上是一种通用的计算工具,在许多其他领域也被广泛应用,例如天气预报和数值稳定性分析等,只是名称不同而已,它的通用名称叫“反向模式微分”(reverse-mode differentiation)。
从本质上看,反向传播是一种快速计算导数的技巧。
计算图
计算图是思考数学表达式的有效方法。以表达式 为例,其中涉及三次运算:两次加法和一次乘法。为了深入讨论这个问题,我们可以引入两个中间变量, 和 。
这样每个函数的输出都有一个变量。我们现在有:
为了创建计算图,我们将每个运算以及输入变量一起放入节点中。当一个节点的值是另一个节点的输入时,箭头会从一个节点连接到另一个节点。
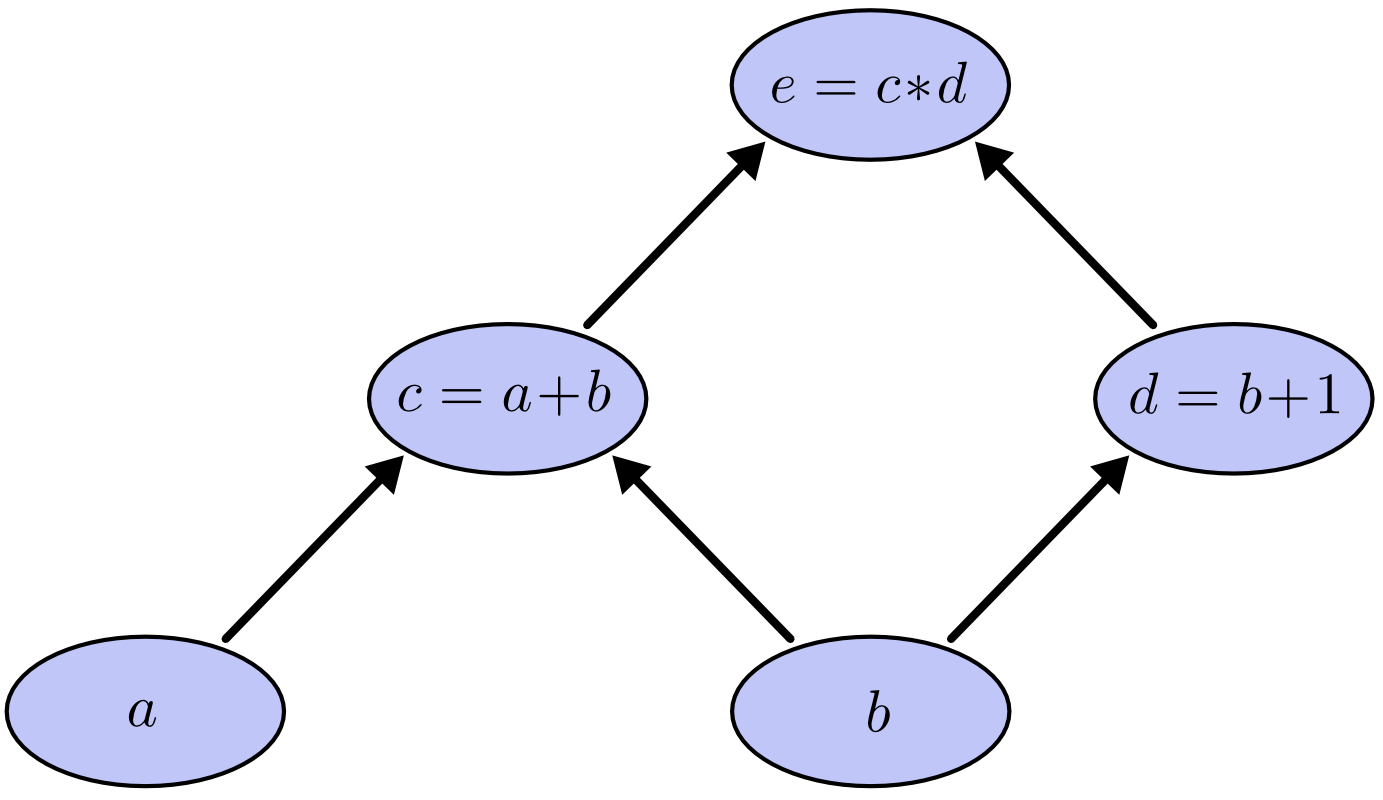
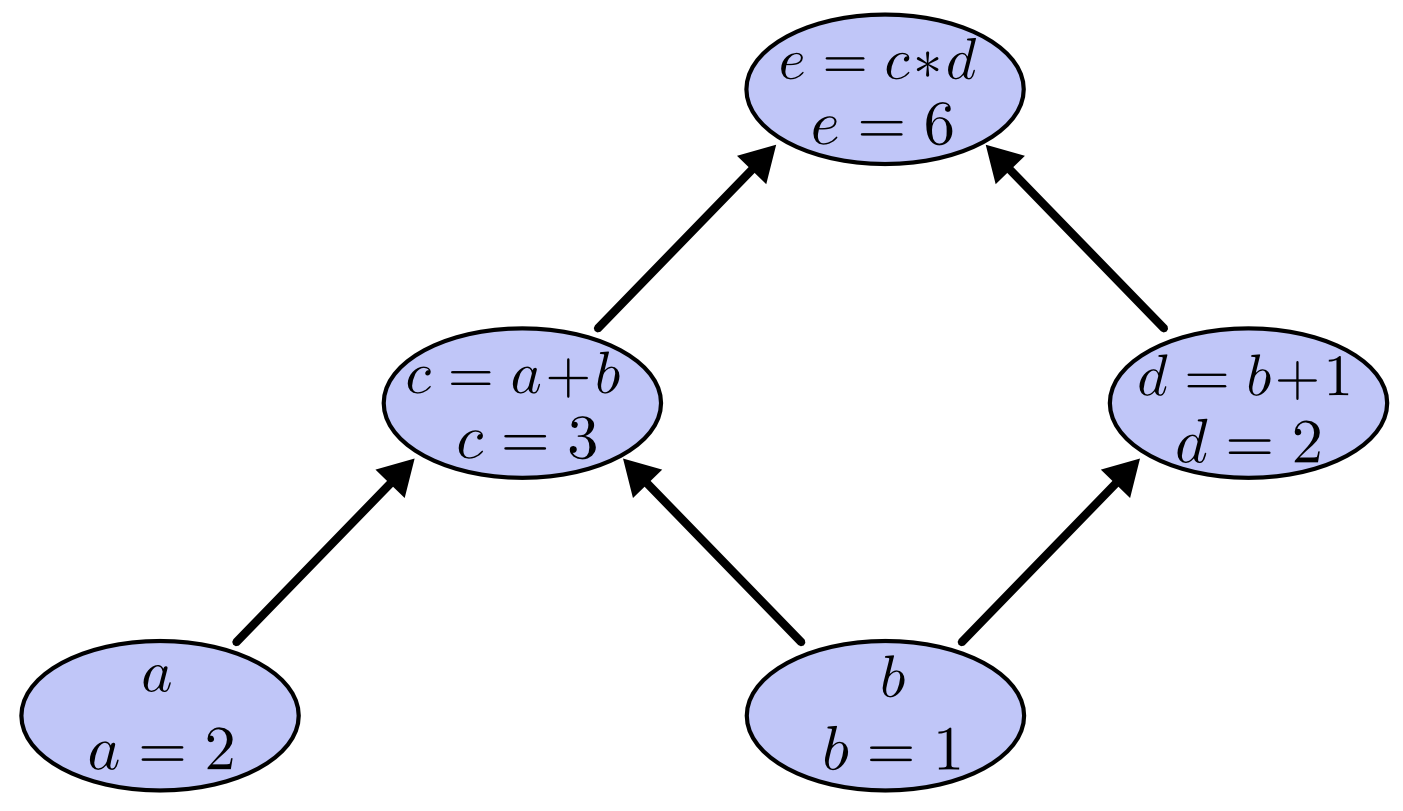
我们可以将输入变量设置为某些特定值,并通过图形计算节点来评估表达式。例如,让我们将 和 作为输入变量的值。
和微积分的关联
反向传播算法主要使用了微积分中的链式法则、乘法法则和加法法则等数学原理。我们结合示例,简单回顾一下这些知识点。
链式法则(chain rule)
链式法则(chain rule)是微积分中的一个重要概念,用于计算复合函数的导数,它帮助我们简化导数的计算,使得我们可以更容易地找到函数的斜率。
假设有一个复合函数 ,其中 是一个单变量函数,那么 的导数可以通过以下方式计算:
这里, 表示函数 在 处的导数, 表示函数 在 处的导数。
链式法则可以扩展到多个函数的复合。
常见函数的导数表可以参考百度百科-导数表
举例说明一
假定 和 。 计算 ,即的导数。
根据链式法则
举例说明二
在图示例子中,, 我们就用到了链式法则来计算 ,我们先可以计算 ,再计算 ,然后两者相乘即得到最后的结果。这样大大方便了计算过程(有动态编程的思想)。后面的图示可以清楚看到。
加法法则
加法法则是指在微积分中,两个函数的和函数的导数等于两个函数的导数的和。具体来说,如果 和 在某一点可导,那么它们的和函数 在该点也可导,且
这个法则可以用于计算复合函数的导数,特别是对于一些简单的函数,可以直接使用加法法则来计算。
例如,假设有一个函数 ,我们需要计算它在 处的导数。根据加法法则,我们可以将这个函数分解为三个部分:,每个部分都可以直接求导,得到 ,将 代入,得到 。
上面的例子中,
加法法则是一个非常基础的微积分法则,它不仅用于计算导数,还可以用于推导更复杂的微积分公式。
乘法法则
微积分中的乘法法则是指,如果两个函数在某一点可导,则它们的乘积函数的导数在该点等于它们的导数的乘积加上它们的乘积。
具体来说,如果 和 在某一点可导,那么它们的乘积函数 在该点也可导,且 。
综合运用链式法则和乘法法则,我们推导一下上面的例子中 是两条路径上的导数乘积的和。 这里
根据基本求导公式:
根据乘法公式和简单替换求得:
计算图上的导数
如果想在计算图中理解导数,关键是要理解边的导数。图中 直接影响 ,那么我们想知道它如何影响 。如果 稍微改变一点, 如何变化?我们称之为 关于 的偏导数。
为了评估此图中的偏导数,我们综合运用链式法则、加法法则、乘法法则。下图在每个边上标记了导数。
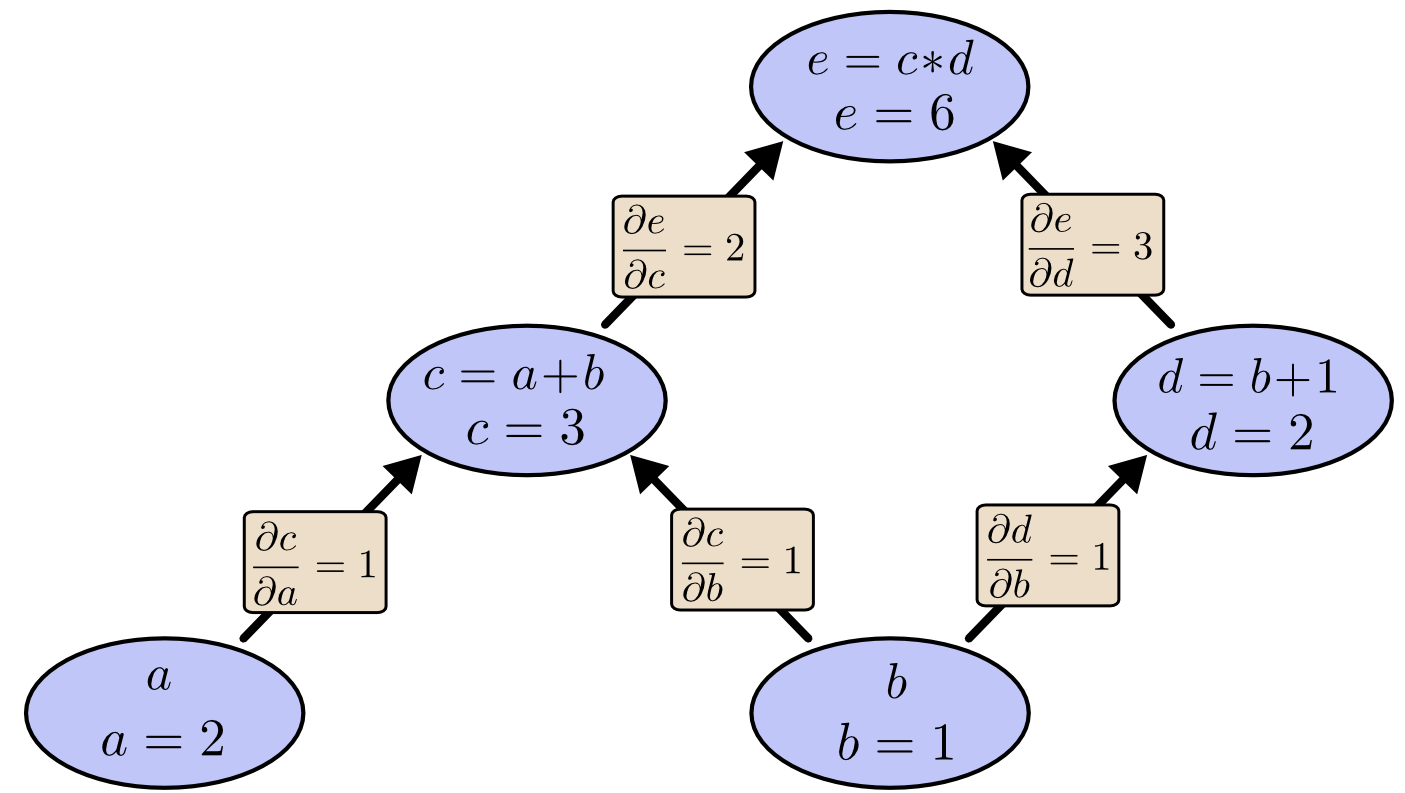
对于未直接连接的节点如何相互影响?让我们考虑 如何受到 的影响。如果我们以 1 的速度改变 , 也会以 1 的速度变化。 以 1 的速度变化会导致 以 2 的速度变化。因此 e 以 的速率相对于 。
一般规则是对从一个节点到另一个节点的所有可能路径求和,将路径每条边的导数相乘。例如,要得到 的导数 关于 ,我们得到:
这解释了 如何通过 和 影响 。
这种一般的“路径求和”规则只是思考多元链规则的一种不同方式。
Pytorch 的自动微分机制和代码示例
PyTorch的一个核心功能是提供自动微分(Autograd),这意味着PyTorch可以自动计算张量间运算的导数。
PyTorch中的张量(Tensor)具有requires_grad属性。当这个属性设置为True时,PyTorch会跟踪对这个张量的所有运算,建立一个计算图,以记录数据和运算之间的关系。
通过调用backward()来自动计算导数。PyTorch会按照计算图进行反向传播,计算每个张量相对于输出的导数。
例如,如果我们想优化输入 x 使得输出 y(一般为损失)最小化,只需要计算 y 关于 x 的导数,并更新 x 按照梯度下降。PyTorch 的 Autograd 可以自动帮我们计算这个导数。
PyTorch 建立计算图的方式对用户完全透明。我们只需要操作张量,不需要手动定义计算图。这简化了代码,也让 PyTorch 可以进行动态计算图,因为每次迭代可以有不同的计算流程。
另外,PyTorch 提供各种优化函数,可以基于 Autograd 计算的梯度自动更新参数。这使得训练神经网络变得极为简单。
总之,PyTorch 的 Autograd 功能让深度学习模型训练变得非常简单和高效。它允许我们只关注模型本身的设计,而不需要关注反向传播与梯度计算的实现细节。
参考:
图示中的例子基于Pytorch的实现如下。
# PyTorch 可以跟踪张量的运算构建计算图,自动计算梯度,并可以方便地访问这些梯度来训练神经网络。
import torch
# a 和 b 是设置了 requires_grad=True 的 PyTorch 张量。这表示 PyTorch 会跟踪它们的运算以方便之后计算梯度。
a = torch.tensor(2.0,requires_grad=True)
b = torch.tensor(1.0,requires_grad=True)
c = a + b
d = b + 1
# 将 c 和 d 相乘,结果存储在 e 中。这里 e 相当于一个“损失函数”。
e = c * d
# 开始反向传播。PyTorch 会计算所有 requires_grad=True 的张量相对于 e 的梯度。
e.backward()
# e 相对于 a 的梯度
print(a.grad) # 2.0
# e 相对于 b 的梯度
print(b.grad) # 5.0
前向模式和反向模式微分的区别
“对路径求和”的问题在于,很容易在可能的路径数量上获得组合爆炸。
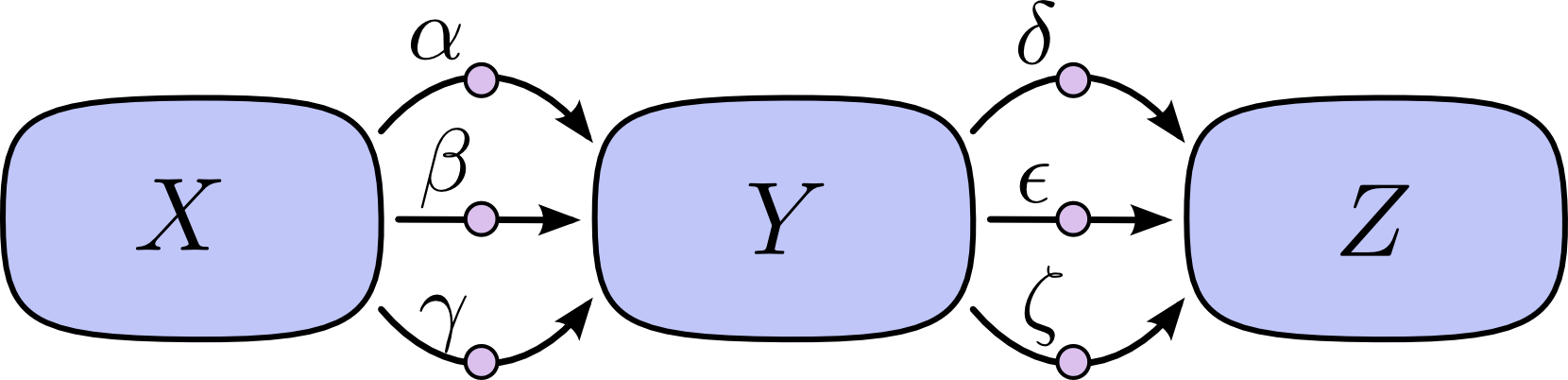
在上图中,从 X 到 Y 有三条路径,从 Y 到 Z 还有三条路径。如果我们想通过对所有路径求和来获得导数 ,我们需要对 路径求和:
上面只有九条路径,但随着图形变得更加复杂,路径的数量很容易呈指数级增长。相较于简单地对所有路径相加,先进行因式分解对计算更友好:
此即“前向模式微分”和“反向模式微分”之由来。此二者均通过分解路径来高效计算:通过在各结点合并路径来计算,而非显式地对所有路径加和。实际上,它俩对每条边均只计算一次。
前向模式微分从输入开始向着最终输出计算,在每个结点都把传入的路径加和,其中每条路径都代表该输入是如何影响结点的。通过加和,我们能得到输入对结点的总影响,即导数。
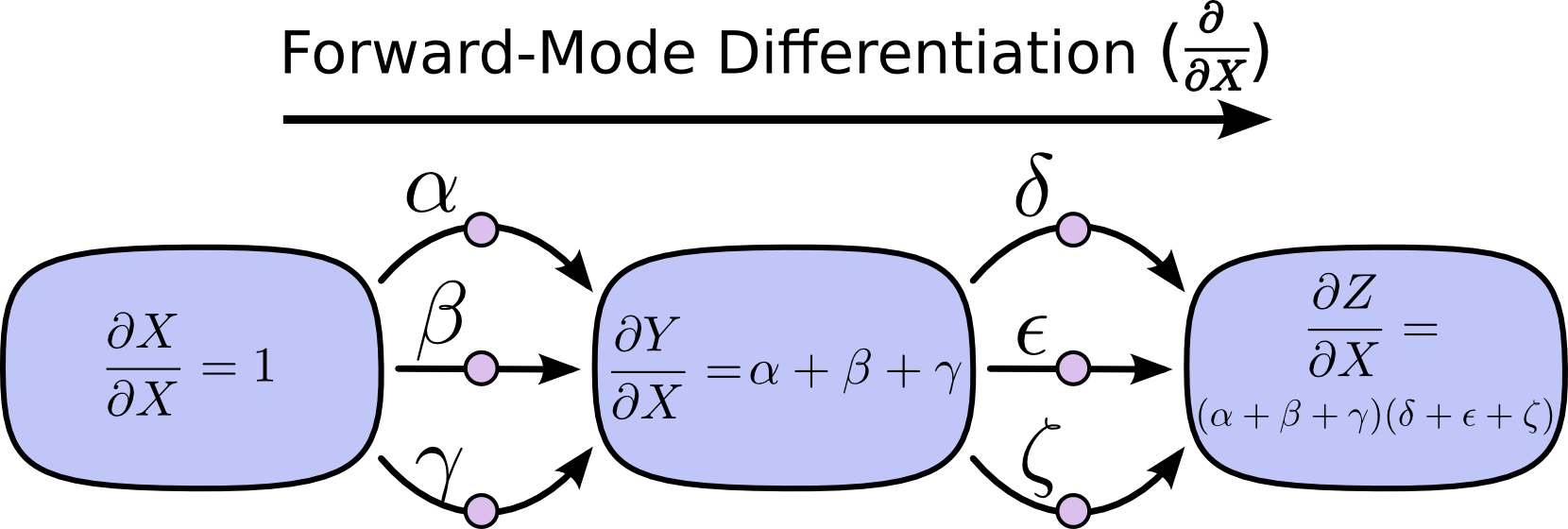
与前向模式微分不同,反向模式微分始于输出,终于输入。在各结点处合并传出于该结点的路径。

前向模式微分考虑的是一个输入如何影响所有结点,而反向模式微分考虑的是所有结点如何影响输出。即,前向模式微分把算子 应用到所有结点,而反向模式微分把算子 应用到所有结点。这个就是动态编程的思想。
计算效率的巨大提升
在这一点上,您可能想知道为什么有人会关心反向模式微分。它看起来像是一种与前向模式做同样事情的奇怪方式。有什么优势吗?
让我们再次考虑我们的原始示例:

我们可以使用前向模式微分从 开始向上计算,得到每个结点关于 的导数。
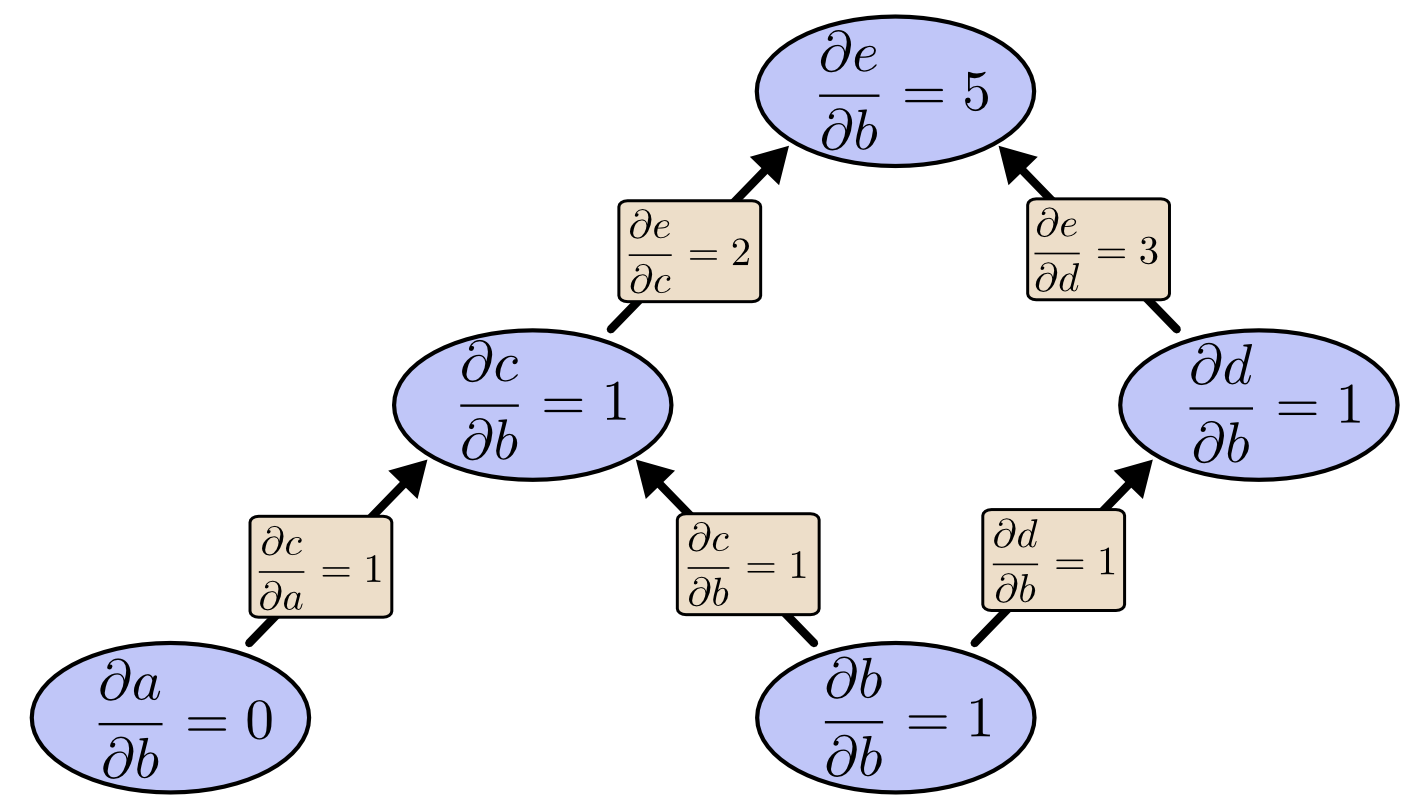
我们计算得到了 ,最终输出关于其中一个输入的导数。
那么我们从 开始做反向模式微分会发生什么呢?这会让我们得到 关于任意结点的导数:
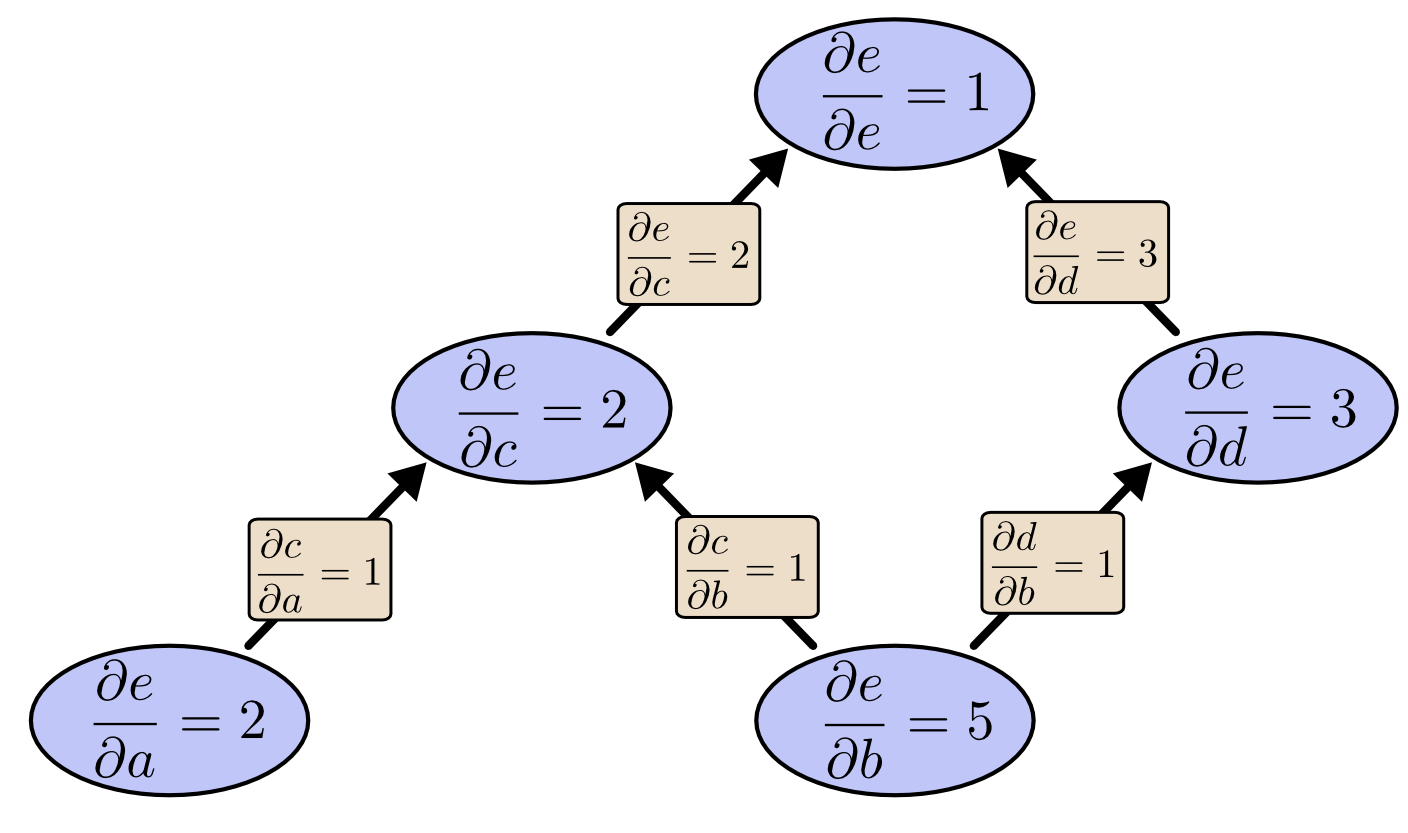
当我说反向模式微分给了我们关于每个节点的 的导数时,我确实是指每个节点。我们得到 和 ,e 的导数
关于这两个输入。正向模式微分为我们提供了输出相对于单个输入的导数,但反向模式微分为我们提供了所有这些导数。
对于此图,这只是速度提升两倍,但想象一下具有一百万个输入和一个输出的函数。正向模式微分需要我们遍历一百万次图才能得到导数。反向模式微分可以一举获得全部!一百万倍的加速是相当不错的!
在训练神经网络时,损失(描述一个网络效果有多差)视为参数(描述网络行为的数字)的函数。我们想要计算损失相对于所有参数的导数,用于梯度下降。现在,神经网络中通常有数百万甚至数千万个参数。因此,反向模式微分,在神经网络的上下文中称为反向传播,为我们提供了巨大的速度!
结论
反向传播算法主要源于微积分中的链式法则、乘法法则和加法法则等数学思想和动态编程思想。
反向传播这个简单的算法(目前看上去)的提出,大幅提升了深度学习中梯度计算的性能,助推了深度学习的蓬勃发展。目前人类已经开始探究AGI的可能性了。
参考论文:
发布于:2023-09-07 11:18:58 描述有误?我来纠错